Single object stereology
The roots of stereology, which may be defined as the statistical inference of geometric parameters from sampled information, are found in the fields of statistics and geometrical probability. Whenever stereology is used to estimate a geometric parameter, it is important to have some idea of how accurate and precise the estimate is. Bias is a measure of the accuracy of an estimator. After an infinite number of trials, an unbiased estimator that exhibits finite variance will converge on the correct (true) result.
The archery targets shown in Figure 1 illustrate the concepts of bias and precision. The objective is to hit the centre of the target. The shots fired at the uppermost targets are unbiased. As the number of shots fired increases, their mean position tends towards the centre of the target. The shots fired at the left-hand targets are precise. Alternatively put, the variance of the set of numbers representing the distances between each shot and their mean position is small.
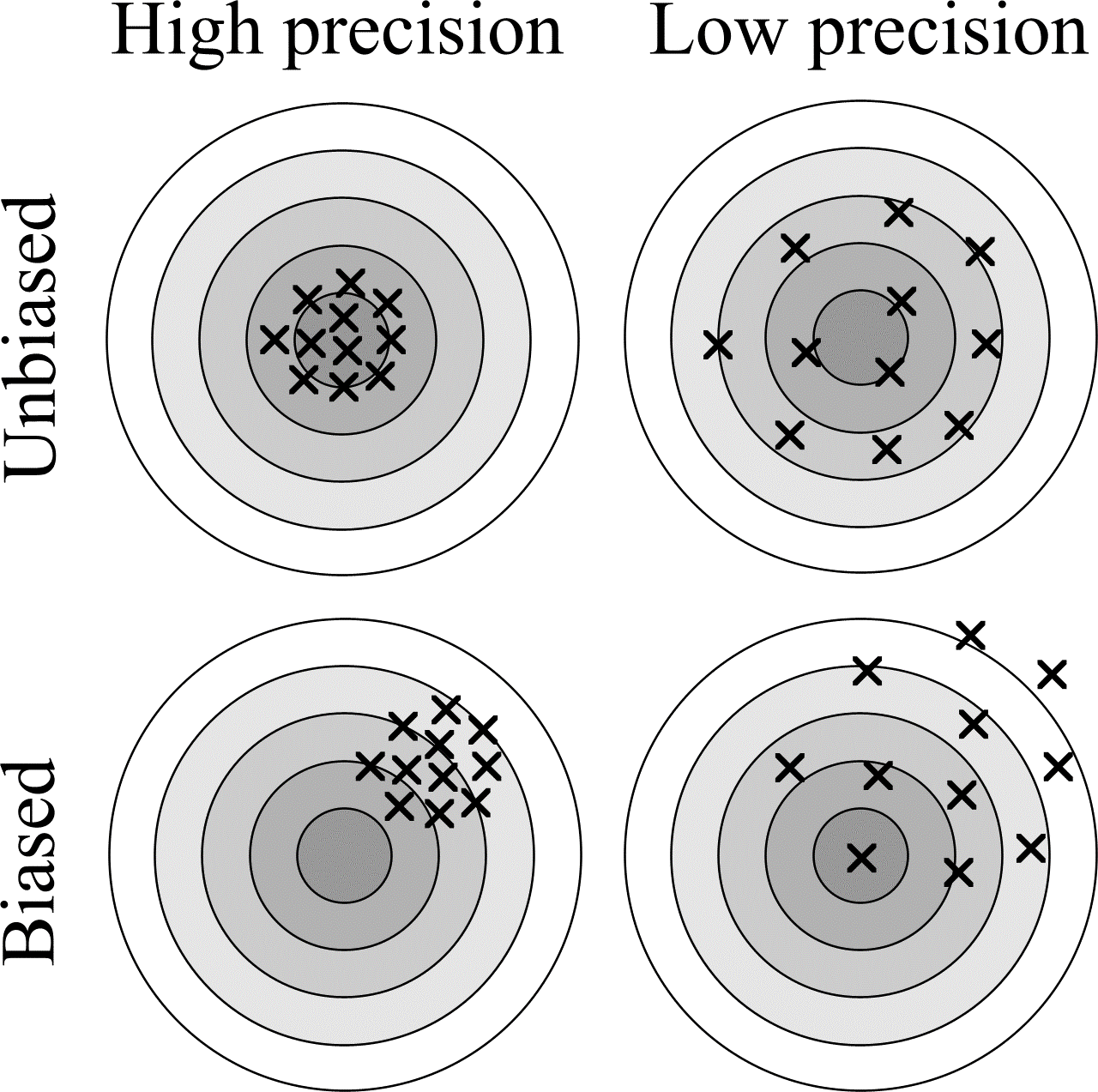
Figure 1: Illustration of bias and precision. The shots fired at the uppermost targets are unbiased, while those fired at the left-hand targets are precise.
The stereological estimators described here are unbiased.
Stereology works by interrogating objects under investigation with geometric test probes such as points, straight lines and curved lines. There are two approaches to stereology - design and model based (Cruz-Orive, 1997; Karlsson and Cruz-Orive, 1992 section 2.2). The design-based approach requires that test probes hit an object (or finite, non-random population of objects) with a well-defined mechanism of randomness. The model-based approach is applicable when the target object (or structure) can be regarded as a realisation of a random set of particles which is homogeneous. For an object to be homogeneous, the mean contents of the object in some window must not depend on the position of the window in space. In this case, test probes may be arbitrarily located as the randomness required to estimate geometric parameters is "contained" within the target object.
As an example of these concepts, consider the problem of determining the area, \(A\), of the unit circle, \(C\). The area is, of course, \(\pi\). One method for tackling the problem is shown in Figure 2(a). \(C\) is broken into strips of width \(\delta x\) and height \(L = \sqrt{1 - x^2} \). The area of the circle is determined by the equation
$$A = 2 \int_{-1}^{1} \sqrt{1 - x^2} \mathrm{d}x = \pi. \tag{1}$$
Suppose a grid of points is overlain on the circle, as shown in Figure 2(b). The total number of points falling within the circle multiplied by the area per point is an unbiased estimate of the area of \(A\). In effect, the systematic sampling of the circle by a grid of points is a numerical integration of (1). The design-based stereological approach, which is employed throughout these notes, stipulates the grid of points must hit the object with a well-defined mechanism of randomness. This is achieved by randomly positioning the grid of points with respect to the stationary circle.
Refinement of the grid, by reducing the distance between points, or taking the average of repeated estimations are two ways of increasing precision. Both methods involve counting more points.
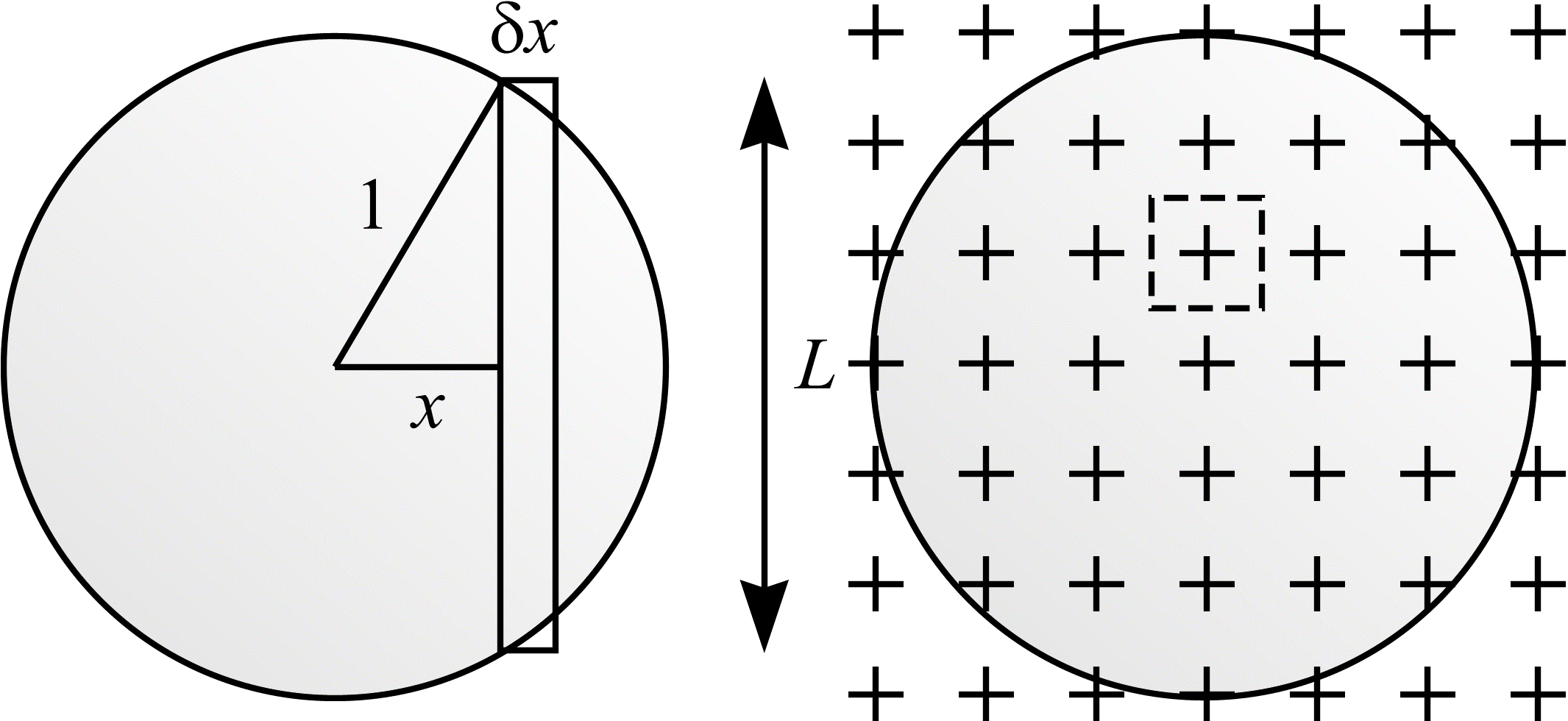
Figure 2: Different methods for calculating the area of the unit circle. (a) The area can be determined by solving the appropriate integral. (b) The area can be estimated by point counting. The dotted square shows the area associated with each point.
These notes summarise some of the fundamental results regarding the stereology of single, bounded objects (Cruz-Orive, 1997). Much of the work is based on a book called Geometrical Probability by Kendall and Moran (1963). The next section describes random variables and this is followed by a discussion concerning the representation of orientations in the plane and in \(\real^3\). This groundwork is followed by the derivations of various stereological estimators.
The problems of area and volume estimation by point counting are considered. An important result, named after the Italian mathematician Bonaventura Cavalieri, is arrived at. The classical two-dimensional (2D) problem of Buffon's needle (1777) is tackled. The theory of Buffon's needle is then applied to the problem of estimating the unknown length of a bounded, rectifiable curve in the plane (Steinhaus, 1930). A curve is rectifiable if it has a well-defined length. Curves that are smooth (infinitely differentiable or \(C^{\infty}\)) are rectifiable. An example of a non-rectifiable curve is the coastline of Britain which exhibits some degree of self-similarity and is said to be fractal (Mandelbrot, 1967).
The extension of Buffon's needle to three dimensions motivates the problems of estimating the length of a bounded rectifiable curve in \(\real^{3}\) (Saltykov, 1946) and of estimating the area of a bounded piecewise smooth surface in three dimensional (3D) space (Saltykov, 1945). Finally, the problem of estimating the length of a bounded rectifiable curve in \(\real^{3}\) from total vertical projections is considered.
References
CRUZ-ORIVE, L. M. Stereology of single objects, J. Microsc., 186, 93-107 (1997).
KARLSSON, L. M. and CRUZ-ORIVE, L. M. The new stereological tools in metallography: estimation of pore size and number in aluminium. Journal of Microscopy, 165, 391-415 (1992).
KENDALL, M. G. and MORAN, P. A. P. Geometrical Probability. London: Ch. Griffin (1963).
MANDELBROT, B. How long is the coast of Britain? Statistical self-similarity and fractional dimension, Science, 636-638 (1967).
SALTYKOV, S. A. Stereometric Metallography, 1st edn. (In Russian). State Publishing House for Metals Sciences, Moscow (1945).
SALTYKOV, S. A. The method of intersections in metallography (In Russian). Zavodskaja laboratorija, 12, 816-825 (1946).
STEINHAUS, H. Zur Praxis der Rektifikation und zum Längenbegriff. Berichte Sächsischen Akad. Wiss. Leipzig, 82, 120-130 (1930).