Buffon's needle problem extended to three dimensions

This section is concerned with Buffon's needle problem extended to three dimensions. Instead of an array of lines (or joints), consider an array of parallel planes, a distance \(h\) apart. In \(\real^{3}\), these planes can be described by \(z = nh\) \((n = 0, \pm 1, \pm 2, ...)\). A needle, length \(l\) \((l < h)\), is thrown into the array of planes. What is the probability, \(\mathbf{P}\), that the needle transects one of the planes?

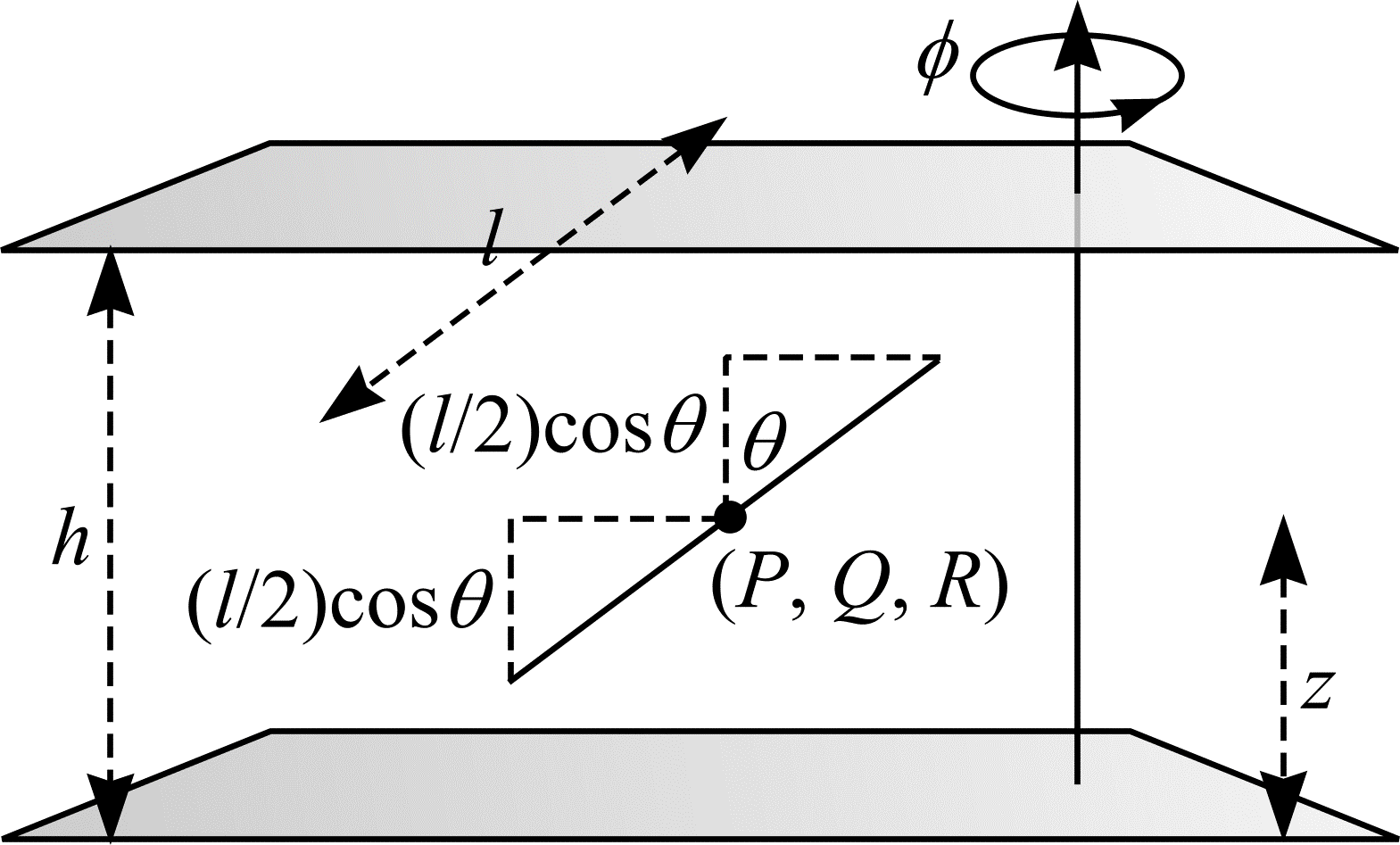
Buffon's needle in three dimensions

Figure 14: Buffon's needle problem extended to three dimensions.

Let \((P, Q, R)\) be the coordinates of the centre of the needle. Let the orientation of the needle be determined by the two angles, \(\Phi\) and \(\Theta\). Denote the distance from the needle's centre and the plane beneath it as \(Z\). The needle is assumed to be IUR in \(\real^{3}\). Therefore \(Z \in \mathrm{UR}[0, h)\), \(\Phi \in \mathrm{UR}[0, \pi)\) and \(\Theta\) is sine weighted in \([0, \pi/2)\). \(Z\) has density function \(f_{Z}(z) = 1/h\). \(\Phi\) has density function \(f_{\Phi}(\phi) = 1/\pi\). \(\Theta\) has density function \(f_{\Theta}(\theta) = \sin\theta\). \(Z\), \(\Phi\) and \(\Theta\) are independent variables and so \(f_{Z, \Phi, \Theta}(z, \phi, \theta) = f_{Z}(z) f_{\Phi}(\phi) f_{\Theta}(\theta)\). Thus, the triple \(Z\), \(\Phi\), \(\Theta\) has joint density function \(f(z, \phi, \theta) = (\sin\theta)/\pi h\).

Figure 14 shows the needle transects a plane if and only if \(z \le (l/2)\cos\theta\) or \(z \ge h - (l/2)\cos\theta\). Clearly, a transect occurring is not dependent upon \(\phi\). Let \(B_{3} = \{(z, \phi, \theta) : z \le (l/2)\cos\theta\) or \(z \ge h - (l/2)\cos\theta\}\). A transect occurs for all \((Z, \Phi, \Theta) \in B_{3}\). A trivial extension of (12) leads to the following:

$$ \begin{align} \mathbf{P} &= \int \int \int_{B_{3}} f(z, \theta, \phi) \mathrm{d}z \mathrm{d}\theta \mathrm{d}\phi \\ &= \frac{1}{\pi h} \int_{0}^{\pi/2} \int_{0}^{\pi} \left( \int_{0}^{(l/2)\cos\phi} \sin\phi \mathrm{d}z + \int_{h - (l/2)\cos\phi}^{h} \sin\phi \mathrm{d}z \right) \mathrm{d}\theta \mathrm{d}\phi \\ &= - \frac{1}{\pi h} \int_{0}^{\pi / 2} \int_{0}^{\pi} \cos \phi \sin \phi \mathrm{d}\theta \mathrm{d}\phi \\ &= \frac{l}{h} \int_{0}^{\pi/2} \cos \phi \sin \phi \mathrm{d}\phi \\ &= \frac{l}{2h}. \end{align} \tag{38} $$
\(\mathbf{P} = \int \int \int_{B_{3}} f(z, \theta, \phi) \mathrm{d}z \mathrm{d}\theta \mathrm{d}\phi = \frac{1}{\pi h} \int_{0}^{\pi/2} \int_{0}^{\pi} ( \int_{0}^{(l/2)\cos\phi} \sin\phi \mathrm{d}z + \int_{h - (l/2)\cos\phi}^{h} \sin\phi \mathrm{d}z ) \mathrm{d}\theta \mathrm{d}\phi \)
\((38)\)

The following work assumes \(h\) is known with \(l\) to be estimated. The needle transects a plane with probability \(l/2h\) and falls between planes with probability \(1 - l/2h\). Consider the discrete random variable \(Q\) that maps the outcomes needle transects a plane and needle falls between planes to the real numbers 1 and 0, respectively. According to (2), \(Q\) has expected value \(\mathbf{E}Q = l/2h\) and therefore

$$ l = 2 \cdot h \cdot \mathbf{E}Q. \tag{39} $$

An estimate of \(l\) can be obtained from a single throw of the needle:

$$ \hat{l} = 2 \cdot h \cdot Q. \tag{40} $$