Documentation
- Images
  - Import
    - Analyze
    - Raw
- Stereology

Exhaustive vertical sectioning

In the case where several series of vertical sections, separated by a distance $T$, sample the object of interest $M$ from one end to the other (i.e. exhaustively), reference volume can be determined from the same images as provide the estimate of surface density. If the Cavalieri estimate of volume (29) is substituted into (45), an equation determining surface area directly by intersection counting is obtained:

$$ \begin{align} S &= 2 \frac{\mathbf{E}I}{\mathbf{E}L} V \\ &= 2 \frac{\mathbf{E}I}{\mathbf{E}P \cdot \left(\frac{l}{p} \right)} \mathbf{E}P \cdot \left( \frac{a}{p} \right) \cdot T \\ &= 2 \cdot \frac{a}{l} \cdot \mathbf{E}I \cdot T \end{align} \tag{49} $$

The best estimates of surface area are achieved if $M$ is sampled systematically. In Figure 22, $M$ is sampled systematically by $n$ = 4 series of vertical sections. Series $i$ ($i = 0 ... n - 1)$ has orientation $\phi_{i} = \phi_{0} + i \cdot (\pi / n)$ where $\phi_{0} \in \mathrm{UR}[0, \pi/n)$. The orientations are shown as dotted lines emanating from an arbitrarily chosen point $P$ on the horizontal plane. In Figure 22, $P$ is positioned near the centre of the projection of $M$ onto the horizontal plane. The offsets, $z_{i}$, for each of the $n$ series of vertical sections are chosen at random without replacement from the set of values $(j/n) \cdot T$ ($0 \le j \lt n)$.

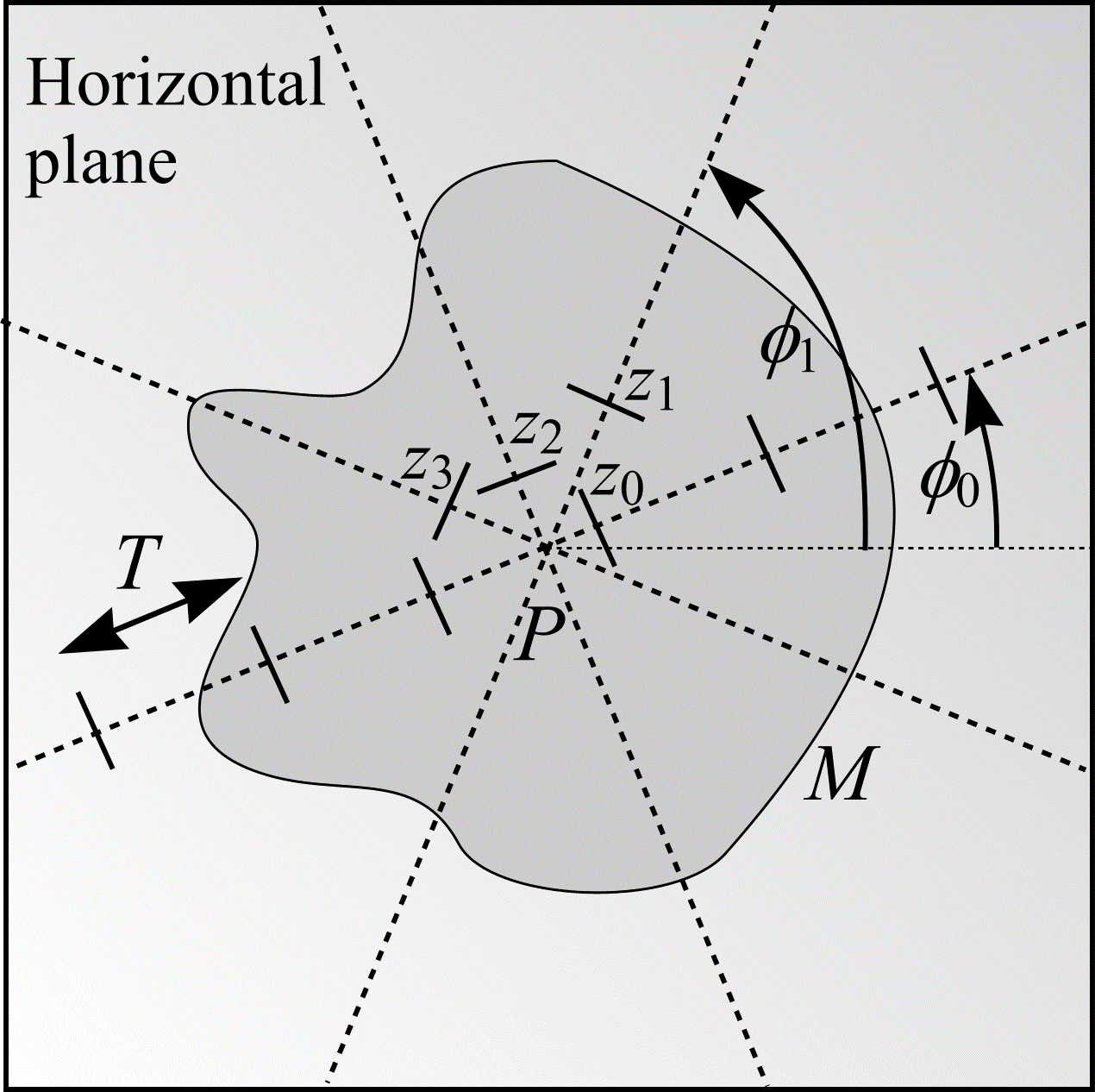
Exhaustive vertical sections

Figure 22: Illustration of a method for obtaining exhaustive vertical sections through a bounded object, $M$. The view is from above $M$, looking down on the horizontal plane. In this example, the number of series of vertical sections, $n$, is 4.

Each series of vertical sections through $M$, with UR test systems of rolling cycloids overlain, contributes an estimate of surface area, $S_{i}$, according to (49). A final estimate of object surface area, $S$, is calculated from the mean of the surface area estimates obtained from each series so that $S = (S_{0} + ... + S_{n})/n$. This result was first recognised by Michel and Cruz-Orive (1988).

References

MICHEL, R. P. and CRUZ-ORIVE, L. M. Application of the Cavalieri principle and vertical sections method to lung: estimation of volume and pleural surface area. J. Microsc., 150, 117-136 (1988).