Curve length in \(\real^3\) from total vertical projections

Total vertical projections (TVPs) can be obtained by fixing a vertical axis with respect to the object under study. Then, with a random starting angle and continuing at uniform intervals, the whole object is projected onto a plane in a systematic set of directions between 0 and \(\pi\) radians. An estimator of curve length from TVPs can be obtained with the help of (43). The following derivation is illustrated in Figure 28.

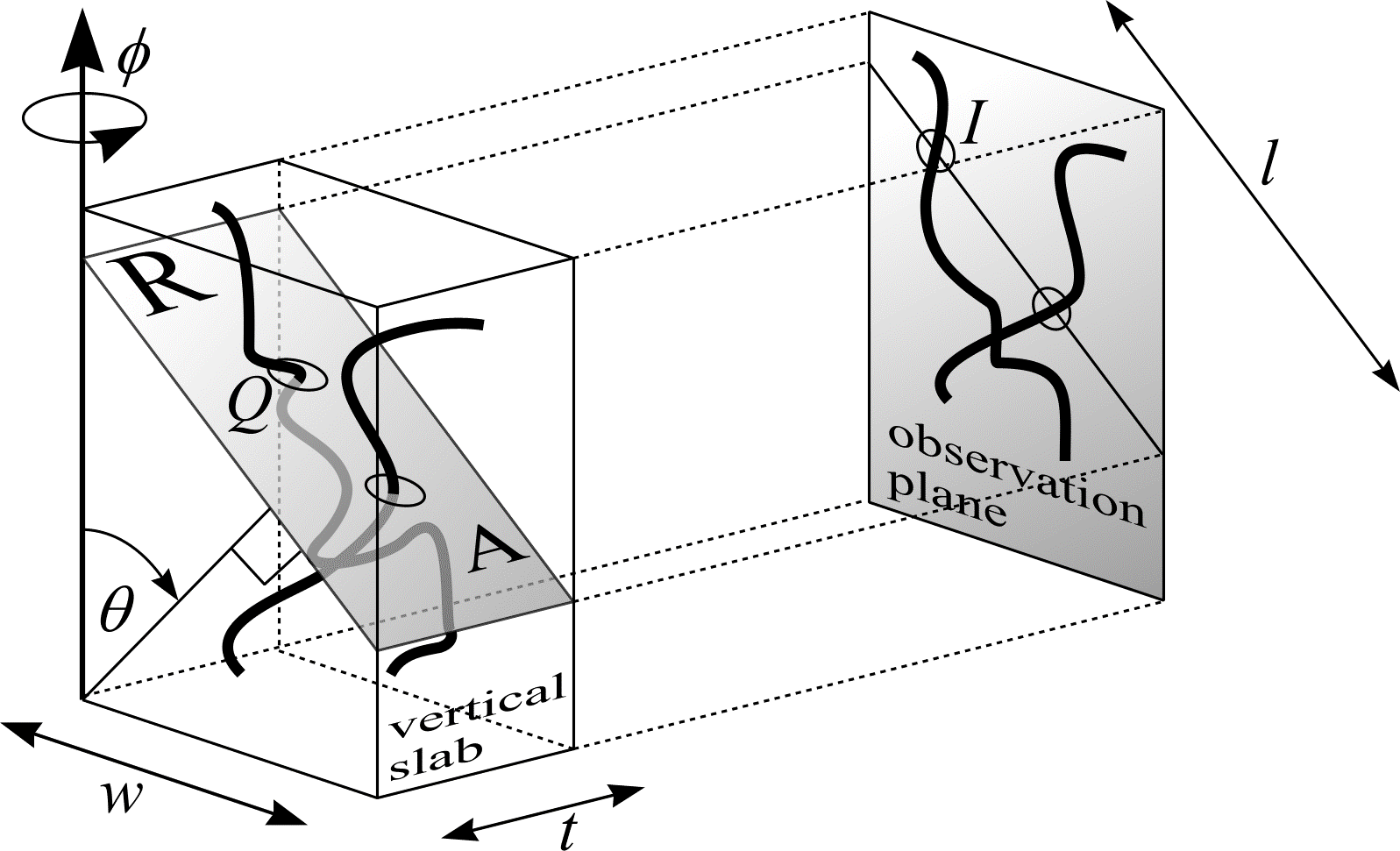
Figure 28: Estimating curve length from total vertical projections. Redrawn from Cruz-Orive (1997).

Consider a curve in \(\real^{3}\), of length \(L\), in a bounded reference space of volume \(V\). Choose an arbitrary horizontal plane with vertical axis perpendicular. Next, sit a vertical slab of known thickness \(t\) and width \(w\) on the horizontal plane. The vertical slab must be positioned so that its rectangular base is IUR in the horizontal plane. Construct a test plane perpendicular to the slab. The test plane must be IUR in \(\real^{3}\). Therefore, the angle \(\theta\) between the normal to the plane and the vertical axis must have probability density function \(\sin\theta\). Furthermore, given \(\theta\), the position of the test plane must be UR on any bounded interval along the normal to the plane. The intersection of the test plane with the vertical slab forms an IUR rectangle, \(R\), whose area is \(t \cdot l\), where \(l = w/cos\theta\). If there are \(Q\) transects between the curve and \(R\), then from (43):

$$ \frac{L}{V} = 2 \frac{\mathbf{E}Q}{t \cdot l}. \tag{53} $$

Project the curve and \(R\) onto an observation plane parallel to the vertical slab. \(R\) becomes a line segment of length \(l\). The line segment is cosine-weighted because its normal is sine-weighted. If there are no overlapping problems the number of transects, \(Q\), between the curve and \(R\) is equal to the number of intersections, \(I\), between the projections of \(R\) and the curve. Equation (53) becomes

$$ \frac{L}{V} = \frac{2}{t} \cdot \frac{\mathbf{E}I}{L}, \tag{54} $$

a result originally obtained by Gokhale (1990). This result has been applied by McMillan et al. (1994) and Batra et al. (1995) to estimate capillary length.

Instead of repeated sampling of cosine-weighted straight lines, it is convenient to use a test system of cycloids with the minor principal axis perpendicular to the vertical axis. Let \(t \to \infty\). The projection is now a total vertical projection (TVP). Onto the TVP superimpose a uniform random test system of (cosine-weighted) cycloids, with known length per unit area \(l/a\). From (54) Cruz-Orive and Howard (1991) obtained:

$$ \begin{align*} L &= 2 \cdot \frac{V}{t} \cdot \frac{1}{l} \cdot \mathbf{E}I \\ &= 2 \cdot \frac{a}{l} \cdot \mathbf{E}I. \end{align*} $$

\(I\) is the total number of intersections between the TVP of the curve and the test system of cycloids on the projection plane. When \(m\) TVPs are obtained, curve length \(L\) is estimated by:

$$ \hat{L} = \frac{2 \cdot \frac{a}{l} \cdot I}{m}. \tag{55} $$

TVPs have been used by Roberts et al. (1991) with MRI to estimate the length of blood vessels, while Howard et al. (1992, 1993) and Roberts and Cruz-Orive (1993) have estimated neuron dendritic length.

References

BATRA, S., KÖNIG, M. F. and CRUZ-ORIVE, L. M. Unbiased estimation of capillary length from vertical slices. J. Microsc., 178, 152-159 (1995).

CRUZ-ORIVE, L. M. and HOWARD, C. V. Estimating the length of a bounded curve in three dimensions using total vertical projections. J. Microsc., 163, 101-113 (1991).

CRUZ-ORIVE, L. M. Stereology of single objects, J. Microsc., 186, 93-107 (1997).

GOKHALE, A. M. Unbiased estimation of curve length in 3D using vertical slices. J. Microsc., 159, 133-141 (1990).

HOWARD, C. V., CRUZ-ORIVE, L. M. and YAEGASHI, H. Estimating neuron dendritic length in 3D from total vertical projections and from vertical slices. Acta Neurol. Scand. Suppl., 137, 14-19 (1992).

HOWARD, C. V., JOLLEYS, G., STACEY, D., FOWLER, A., WALLÉN, P. and BROWNE, M. A. Measurement of total neuronal volume, surface area, and dendritic length following intracellular physiological recording. Neuroprotocols: A Companion to Methods in Neurosciences, 2, 113-120 (1993).

MCMILLAN, P. J., ARCHAMBEAU, J. O., GOKHALE, A. M., ARCHAMBEAU, M. H. and OEY, M. Morphometric and stereologic analysis of cerebral cortical microvessels using optical sections and thin slices. Proc. 6ECS Prague 1993. Acta Stereol., 13/1, 33-38 (1994).

ROBERTS, N., HOWARD, C. V., CRUZ-ORIVE, L. M. and EDWARDS, R. H. T. The application of total vertical projections for the unbiased estimation of the length of blood vessels and other structures by magnetic resonance imaging. Magnetic Resonance Imaging, 9, 917-925 (1991).

ROBERTS, N. and CRUZ-ORIVE, L. M. Spatial distribution of curve length: concept and estimation. J. Microsc., 172, 23-29 (1993).