Buffon's needle

Imagine a room whose floor is made up of planks of wood. The planks have uniform width, \(h\), and are parallel to one another. A needle, length \(b\) \((b < h)\), is thrown into the air. What is the probability, \(\mathbf{P}\), that the needle intersects one of the joints between the planks? This question was first asked by Georges Louis Leclerc, Comte de Buffon (1777).

Suppose the joints are represented by the lines \(y = nh\) \((n = 0, \pm 1, \pm 2, ...)\). Let \((P, Q)\) be the coordinates of the centre of the needle and let \(\Phi\) be the angle, modulo \(\pi\), made by the needle and the \(x\)-axis. Denote the distance from the needle's centre and the nearest line beneath it as \(Z\). The needle is assumed to be IUR. In other words, \(Z \in \mathrm{UR}[0, h)\) and \(\Phi \in \mathrm{UR}[0, \pi)\). \(Z\) has density function \(f_{Z}(z) = 1/h\). \(\Phi\) has density function \(f_{\Phi}(\phi) = 1/\pi\). \(Z\) and \(\Phi\) are independent variables and so \(f_{Z,\Phi}(z, \phi) = f_{Z}(z) f_{\Phi}(\phi)\). Thus, the pair \(Z\), \(\Phi\) has joint density function \(f(z, \phi) = 1/\pi h\).

Figure 10 suggests an intersection between the needle and a joint occurs if and only if \(z \le (b/2)\sin\phi\) or \(z \ge h - (b/2)\sin\phi\). Let \(B_{2} = \{(z, \phi) : z \le (b/2)\sin\phi\) or \(z \ge h - (b/2)\sin\phi\}\). An intersection occurs for all \((Z, \Phi) \in B_{2}\). From Equation (12),

$$ \begin{align} \mathbf{P} &= \int\int_{B_{2}} f_{Z, \Phi}(z, \phi)\mathrm{d}z\mathrm{d}\phi \\ &= \frac{1}{\pi h} \int_{0}^{\pi} \left( \int_{0}^{(b/2)\sin\phi} \mathrm{d}z + \int_{h - (b/2)sin\phi}^{h} \mathrm{d}z \right) \mathrm{d}\phi \\ &= \frac{2b}{\pi h}. \end{align} \tag{31} $$
\(\mathbf{P} = \int\int_{B_{2}} f_{Z, \Phi}(z, \phi)\mathrm{d}z\mathrm{d}\phi \\ = \frac{1}{\pi h} \int_{0}^{\pi} ( \int_{0}^{(b/2)\sin\phi} \mathrm{d}z + \int_{h - (b/2)sin\phi}^{h} \mathrm{d}z ) \mathrm{d}\phi \\ = \frac{2b}{\pi h}.\)
\((31)\)

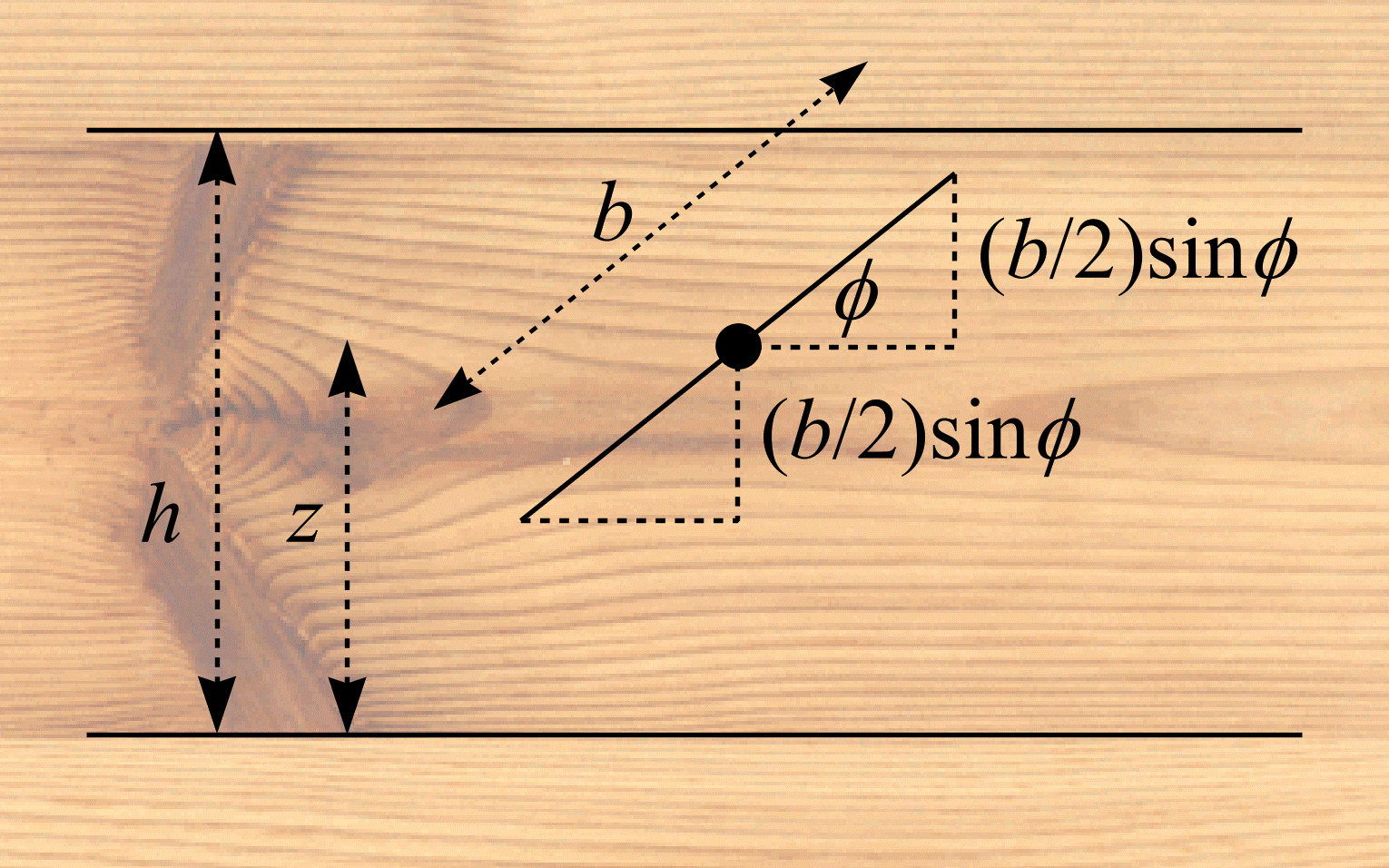
Buffon's needle

Figure 10: Buffon's needle.

When \(b\) and \(h\) are known quantities, (31) can be used to estimate the numerical value of \(\pi\). This was the original intention of Buffon. The following work assumes \(h\) and \(\pi\) are known with \(b\) to be estimated.

Suppose the needle is thrown and lands on the floor. The needle intersects a joint with probability \(2b/\pi h\) and falls between joints with probability \(1 - 2b/\pi h\). Consider the discrete random variable \(I\) that maps the outcomes needle intersects a joint and needle falls between joints to the real numbers 1 and 0, respectively. According to (2), \(I\) has expected value \(\mathbf{E}I = 2b/\pi h\) and therefore

$$ b = \frac{\pi}{2} \cdot h \cdot \mathbf{E}I. \tag{32} $$

An estimate of \(b\) can be obtained from a single throw of the needle:

$$ \hat{b} = \frac{\pi}{2} \cdot h \cdot I. \tag{33} $$

References

BUFFON, G. L. L. Comte de. Essai d'Arithmétique Morale. In: Supplément à l'Histoire Naturelle, v. 4. Paris: Imprimerie Royale (1777).