Vertical sections

It is often more convenient to estimate surface area from vertical sections. A vertical section, as shown in Figure 20, is a section that is perpendicular to an arbitrary chosen horizontal plane and its intersection with the horizontal plane is an IUR line on the horizontal plane. On anatomical datasets, coronal, sagittal and sagittal-oblique sections can be obtained as vertical sections when the horizontal plane is an axial section.

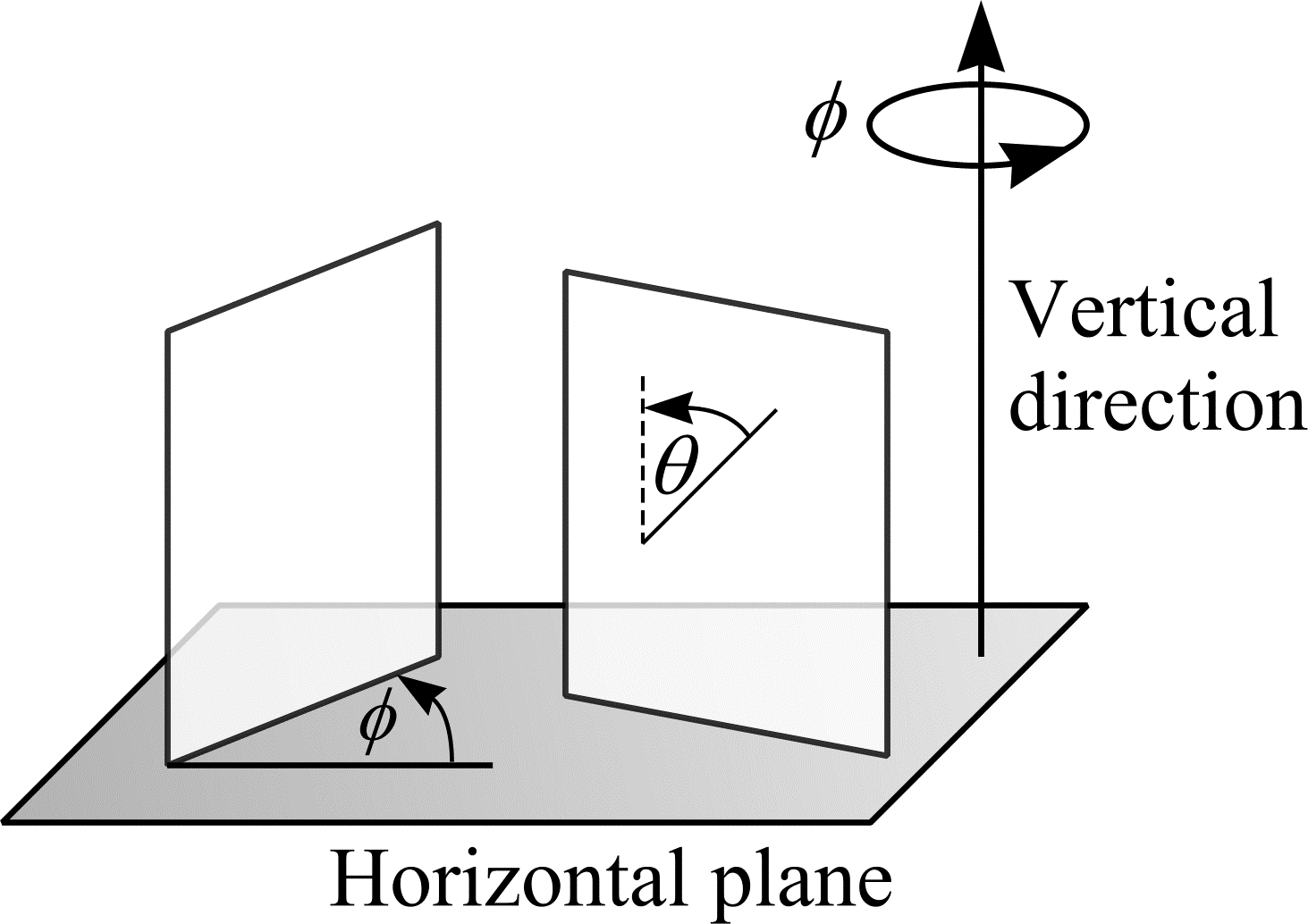
Figure 20: Vertical sections

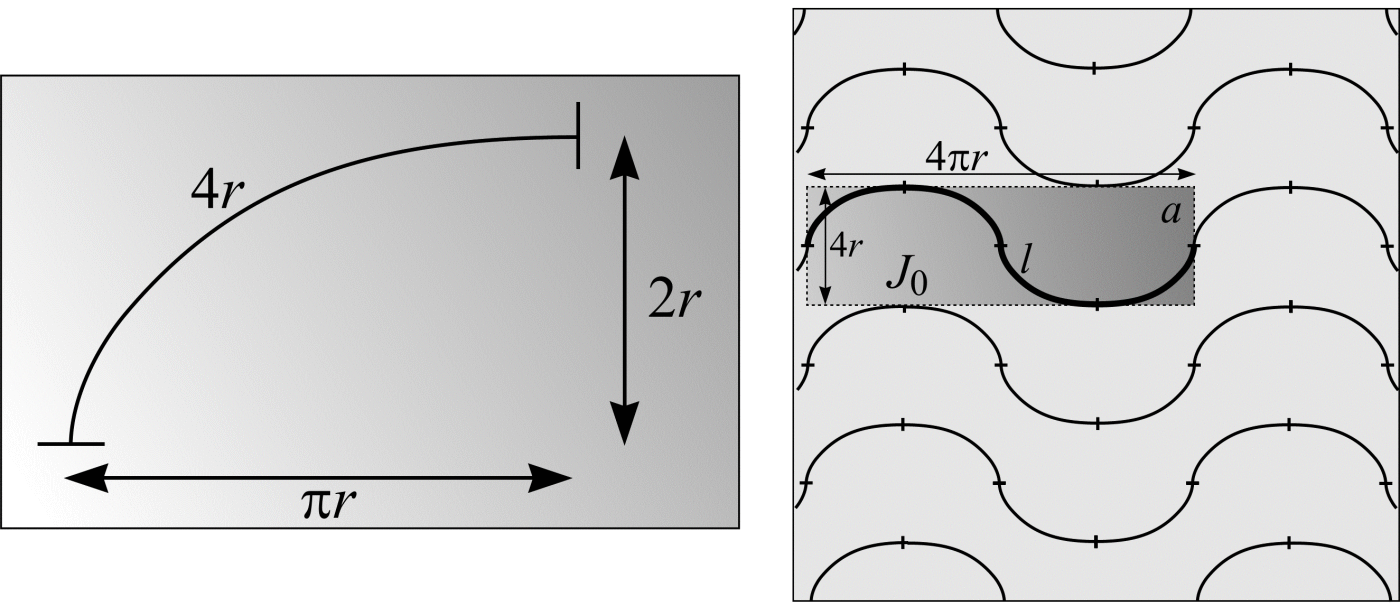
Any straight line in \(\real^{3}\) can be contained in a vertical section. Therefore, any stereological procedure requiring IUR test lines, such as (46), may be implemented using vertical sections as supports for the lines. As shown previously, a test line on a vertical section is effectively IUR in \(\real^{3}\) if the angle \(\theta\) between the test line and the vertical direction has probability density function \(\sin\theta\) and, given \(\theta\), the position of the test line is uniform random on any bounded interval perpendicular to the test line. Thus, a uniform random sine-weighted line on a vertical section is effectively IUR in \(\real^3\). Instead of repeated sampling of sine-weighted straight lines on a vertical section it is convenient to use a test curve that encapsulates the sine weighting property for all \(\theta\) (\(0 \le \theta \lt \pi\)), in the sense that the length of element of arc \(\mathrm{ds}(\theta)\) whose tangent makes an angle \(\theta\) with the vertical, is proportional to \(\sin\theta\). The cycloid (illustrated in Figure 21(a)), aligned with its minor axis parallel to the vertical direction, of classical geometry is such a curve (Baddeley et al., 1986).

Figure 21: (a) A cycloid, parametrically defined as: \(x(\theta) = (\theta - \sin\theta)r\) and \(y(\theta) = (1 – \cos\theta)r\) with \(0 \le \theta \le \pi\). (b) A test system of rolling cycloids or cycloid chains (Cruz-Orive and Howard, 1995).

Given vertical sections through a structure with UR cycloids overlain, (46) can be used to estimate the surface density. \(I\) denotes the number of intersections between the boundary of the surface of interest on the sections and the cycloids and \(L\) the length of cycloid within the structure. Suppose a point is marked at the beginning of each cycloid. The length of cycloid associated with each point, \(l/p\), is \(4r\). If the expected number of points falling within the object is \(\mathbf{E}P\), the length of \(L\) is \(\mathbf{E}P \cdot (l/p)\).

A better estimate of the surface density is achieved if the cycloids are systematically placed on the vertical sections. Figure 21(b) shows a UR test system of rolling cycloids a distance \(4r\) apart. A rolling cycloid is defined as

$$ x(\theta) = (\theta - \sin\theta)r \tag{47} $$

and

$$ y(\theta) = \left((1 - \cos\theta)r\right) \cdot (-1)^{[0/2\pi]} \tag{48} $$

where \([x]\) means the integer part of \(x\). The test system can be thought of as a tessellation constructed from a mosaic of fundamental tiles, \(J_{0}\). \(J_{0}\) occupies an area \(a = 4 \pi r \cdot 4r\) and contains a length of rolling cycloid, \(l = 16r\). Therefore, the test system has length per unit area, \(l/a = 16r/(4 \pi r \cdot 4r) = 1/\pi r\).

References

BADDELEY, A. J., GUNDERSEN, H. J. G. and CRUZ-ORIVE, L. M. Estimation of surface area from vertical sections. J. Microsc., 142, 259-276 (1986).

CRUZ-ORIVE, L. M. and HOWARD, C. V. Estimation of individual feature surface area with the vertical spatial grid. J. Microsc., 178, 146-151 (1995).