Surface density

Equation (43) says that the length of \(C\) per unit volume is equal to twice the number of transects between \(C\) and the test system, per unit area of test system. The dual situation can be conceived if the test system is replaced by a stationary, bounded object in \(\real^{3}\), \(M\), whose surface area is \(S\) and whose volume is \(V\). Suppose \(S\) and \(V\) are unknown. \(L/V\) is then the length of \(C\) lying within \(M\), while \(\mathbf{E}Q/A\) becomes the number of intersections between \(C\) and \(M\), per unit area of \(M\). By an additional change of notation of \(A\) into \(S\) and of \(Q\) (transect of \(C\) with a plane) into \(I\) (intersection produced by \(C\) in a surface) the following is obtained:

$$ \begin{align} \frac{L}{V} &= 2 \cdot \frac{\mathbf{E}Q}{A} \\ \iff \frac{A}{V} &= 2 \cdot \frac{\mathbf{E}Q}{L} \\ \iff \frac{S}{V} &= 2 \cdot \frac{\mathbf{E}I}{\mathbf{E}L}. \end{align} \tag{45} $$

Equation (45) determining the surface density, \(S/V\), of \(M\) is another fundamental equation of stereology originally obtained by Saltykov (1945). In practise, the (test) curve \(C\) is replaced by an IUR test system of test lines. \(I\) and \(L\) are random variables. \(I\) denotes the number of intersections between the object surface and the test lines, \(L\) the length of test lines falling within the object.

An IUR line in \(\real^{3}\) that passes through \(M\) can be generated as follows. Let \(u_{1} \in \mathrm{UR}[0, 1)\), \(u_{2} \in \mathrm{UR}[0, 1)\), \(u_{3} \in \mathrm{UR}[0, 1)\) and \(u_{4} \in \mathrm{UR}[0, 1)\). Construct a line or isotropic axis with orientation \(\theta = \cos^{-1}(1 - 2u_{1})\) and \(\phi = \pi u_{2}\). As shown in Figure 16, fix a plane perpendicular to the isotropic axis and project the object, \(M\), onto that plane. Draw a square on the plane (side length \(l\)), which contains the projection of \(M\). From a point that has UR position within the square, namely \((u_{3}\cdot l, u_{4}\cdot l)\), draw a second axis perpendicular to the plane. If this axis hits \(M\) (i.e. the point \((u_{3}\cdot l, u_{4}\cdot l)\) is contained within the projection of \(M\)), then it can be considered an IUR line in \(\real^{3}\) that passes through \(M\). Otherwise the procedure must be restarted with 4 new random numbers.

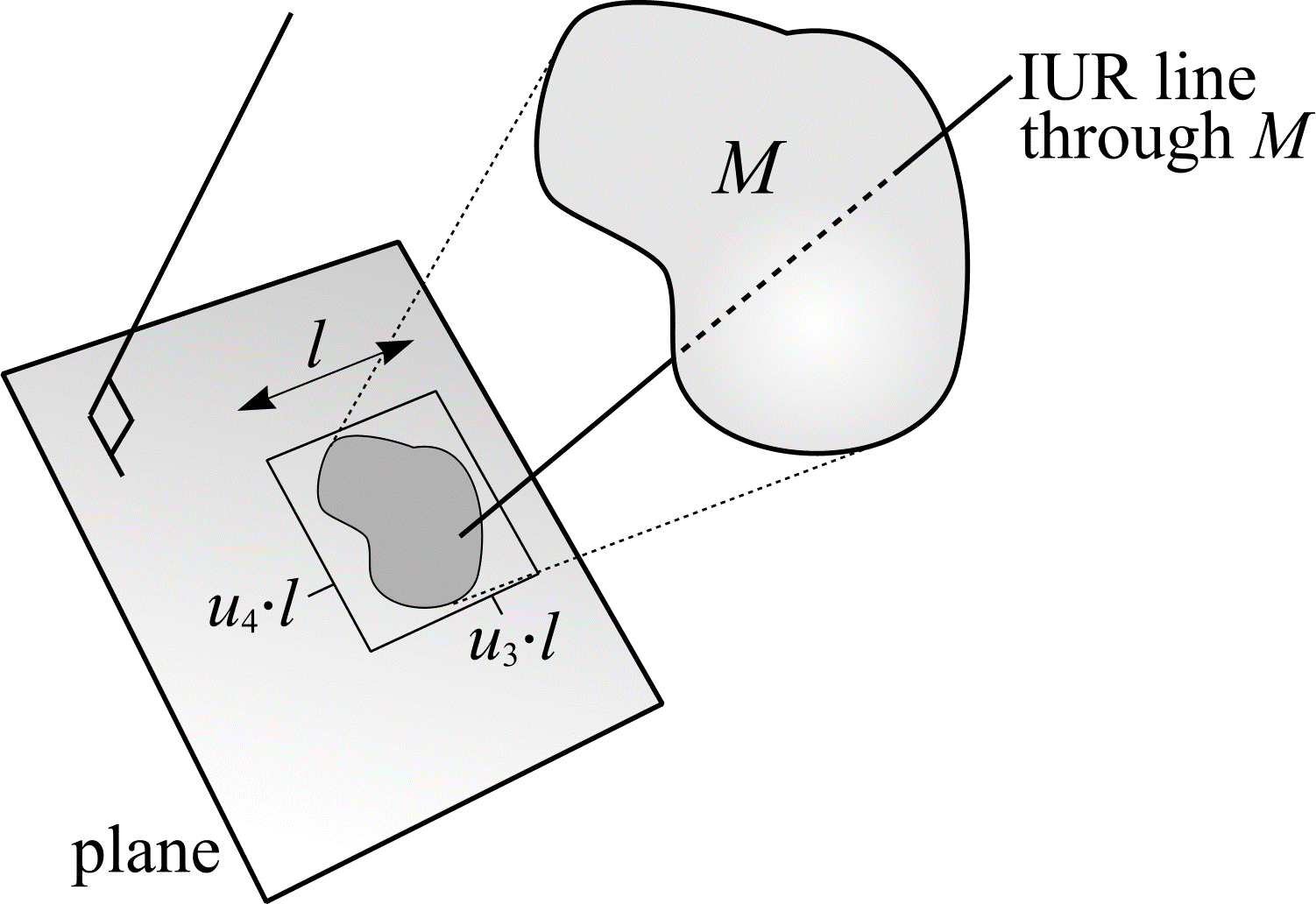
Figure 16: The construction of an IUR line.

Suppose a UR systematic set of points, a distance \(u\) apart, are positioned along each IUR test line. The length of test line associated with each point, \(l/p\), is \(u\). If the expected number of points falling within the object is \(\mathbf{E}P\), the length of \(L\) is \(\mathbf{E}P \cdot (l/p)\) (see Figure 17). Therefore, an estimate of \(S/V\) can be obtained from a single throw of the IUR test line system:

$$ \begin{align} \text{est } \frac{S}{V} &= 2 \cdot \frac{I}{L} \\ &= 2 \cdot \frac{I}{\left(\frac{l}{p} \cdot P \right)}. \end{align} \tag{46} $$

Figure 17: A method for estimating the length, \(L\), of test line falling within an object. In this example, the object is a sphere and an unbiased estimate of \(L\) is 3\(u\).

References

SALTYKOV, S. A. Stereometric Metallography, 1st edn. (In Russian). State Publishing House for Metals Sciences, Moscow (1945).